移动周分享-第60期

移动组周技术分享

微信-支付宝-银联支付对比 - 王胜

微信支付

业务流程

pay-weixin-timeline

支付宝

业务流程

pay-alipay-timeline

银联

业务流程

pay-unionpay-timeline

结论

支付平台 流程图 文档 接口设计 demo 测试相关
微信 ♥♥♥♥♥ ♥♥♥♥♥ ♥♥♥♥♥ ♥♥♥ ♥♥♥♥
支付宝 ♥♥♥♥ ♥♥♥ ♥♥♥♥ ♥♥ ♥♥
银联 ♥♥♥ ♥♥ ♥♥ ♥♥ ♥♥♥♥

说明：

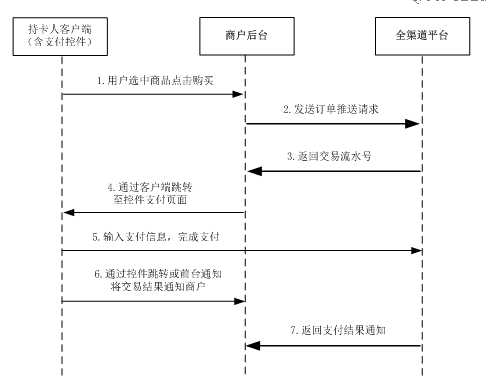
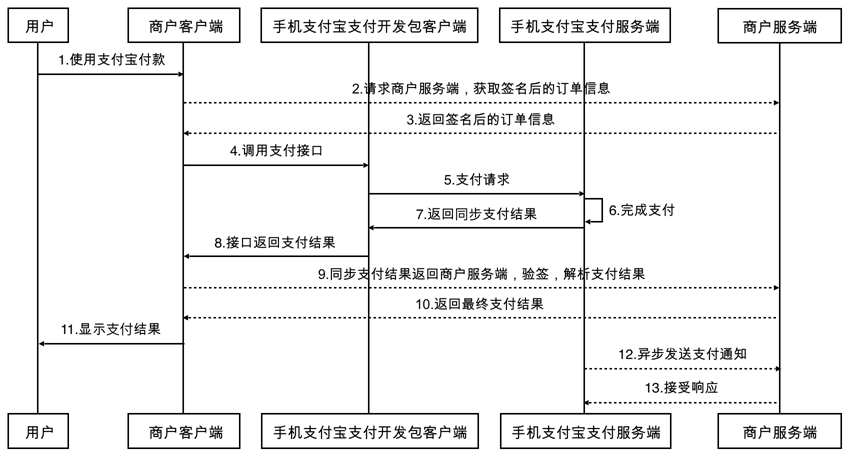
  • 路程图

    从全面性和完整性看，微信 > 支付宝 > 银联

  • 文档：

    微信更简洁，清晰，完整；其他两家还是相对传统的风格，尤其是银联

  • 接口设计：

    微信的接口设计更简洁灵活易用，支付宝次之，银联的字段说明另类。

  • demo:

    微信demo还算清楚，但是美中不足项目编码非utf-8，还得用Notepad++才正确编码显示；支付宝和银联的demo看起来晕。

  • 测试：

    微信的测试环境是通过添加沙箱sandbox路径实现；另外，微信提供了测试用例，赞一个。支付宝没有看到有测试环境。银联在sdk的API参数中，提供了环境参数设置。

iOS响应者链与hit-testing - 刘康

今天我们来探索一下，当我们点击微信扫一扫就能打开扫码视图，当我们点击屏幕的时候。背后发生了些什么？

当用户通过以上方式触发一个事件时，会将相应的事件对象添加到UIApplication的事件队列中。UIApplication会循环的从队列中拿出第一个事件来处理。首先将该事件分发给UIApplication的主窗口对象(KeyWindow)，然后由主窗口决定如何将事件交给最合适的响应者(UIResponder)来处理取决于事件的类型。这里主要分两种情况：

触摸事件

UIApplication通过一个触摸检测来决定最合适来处理该事件的响应者，一般情况下，这个响应者是UIView对象。
对于触摸事件，window对象会尝试着首先将事件传递给触摸事件发生点得View。这个View被视为“命中测试view” (hit-test view)。

手势和远程控制事件

UIApplication寻找UIWindow中的第一响应者。找到第一响应者(The First Responder)后，会将该事件对象派发给该响应者以便处理。

事件传递响应链

最终所有的事件响应路径都是为了去寻找那个能够响应并处理该事件的对象。因此，UIkit会首先发送该事件给最适合处理该事件的对象。对于触摸事件，这个最适合处理的对象就是 hit-test view既“命中测试view”,并且对于其它事件，这个对象就是“第一响应者”。

命中测试返回触摸事件发生点的view

系统检测到手指触摸(Touch)操作时会将其放入当前活动Application的事件队列，UIApplication会从事件队列中取出触摸事件并传递给key window处理,window对象首先会使用hitTest:withEvent:方法寻找此次Touch操作初始点所在的视图(View),即需要将触摸事件传递给其处理的视图:

为了去阐明这个过程，假设用户触摸 view E 如图所示。iOS会以这样的顺序去寻找命中测试view通过检测所有的子view.
Alt text

  1. 触摸点是否在view A的边界之内，如果是它会检测子视图B和C.

  2. 触摸点不在view B的边界之内，但是它在view C的边界之内，因此它就去检测C的子视图D和E。

  3. 触摸事件不在view D的边界之内，但是在view E的边界之内。view E是整个包含触摸事件的view层级中最底端的view，因此view E就名正言顺的成为了“命中测试view”。

例外
不满足一下三个条件的Responder是不能接收触摸事件的：

  • 不允许交互：userInteractionEnabled = NO
  • 隐藏：如果把父控件隐藏，那么子控件也会隐藏，隐藏的控件不能接受事件
  • 透明度：如果设置一个控件的透明度<0.01，会直接影响子控件的透明度。alpha：0.0~0.01为透明。

注意点
一个触摸事件对象将会被关联于命中测试view的整个生命周期，即使这个触摸后来移到了view的边界之外。

实例

  1. 在此例子中button,scrollview同为topView的子视图，但scrollview覆盖在button之上，这样在在button上的触摸操作返回的hit-test view为scrollview,button无法响应，可以修改topView的hitTest:withEvent:方法如下:
1
2
3
4
5
6
7
8
9
- (UIView *)hitTest:(CGPoint)point withEvent:(UIEvent *)event
{
    UIView* result = [super hitTest:point withEvent:event];
    CGPoint buttonPoint = [_checkedButton convertPoint:point fromView:self];
    if ([_checkedButton pointInside:buttonPoint withEvent:event]) {
        return _checkedButton;
    }
    return result;
}
  1. 放弃自身响应，让子视图去响应事件：
1
2
3
4
5
6
7
8
- (UIView*)hitTest:(CGPoint)point withEvent:(UIEvent *)event{
    //当事件是传递给此View内部的子View时，让子View自己捕获事件，如果是传递给此View自己时，放弃事件捕获
    UIView* __tmpView = [super hitTest:point withEvent:event];
    if (__tmpView == self) {
        return nil;
    }
    return __tmpView;
}
  1. 扩大按钮可点击区域：
1
2
3
4
5
6
7
8
9
- (UIView*)hitTest:(CGPoint) point withEvent:(UIEvent*) event
{
    CGRect rect = [self enlargedRect];
    if (CGRectEqualToRect(rect, self.bounds))
    {
        return [super hitTest:point withEvent:event];
    }
    return CGRectContainsPoint(rect, point) ? self : nil;
}

加速库在数学运算中的使用 - 杨志平

@(iOS)[加速|Accelerate]

除了加减乘除外还有好多好多数学运算需要我们处理，但我们很多都没有用到，感觉low爆了

Apple：加速框架文档

Any time you’ve got to make some numbers happen, it’s probably worth it to consider using Accelerate

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 模拟随机数据
var doubles  = (0...10000).map {_ in Double(arc4random()%10000)}

// 求和
// 常见的加法求和
let reduceSum = doubles.reduce(0) { $0+$1 }
// Accelerate 封装
let accSum = sum(doubles)

// 求最大值（最小值也一样）
let maxOfArr = max(doubles)
let maxOfArr2 = doubles.sort(>).first

// 平均值,哈哈大数据统计，可以测试准确率
let meanValue = mean(doubles)
let meanValue2 = doubles.reduce(0) { $0 + $1/Double(doubles.count) }
meanValue2

// 向量加减乘积
let vector1 = [2,4,5] as [Double]
let vector2 = [3,5,2] as [Double]
let sumArrs = add(vector1, y: vector2)

耗时上对比是不是reduce，map等系统的高阶函数被“加速库”秒了，但使用上貌似reduce，map是比较灵活的

1
2
let newReduceSum = (0...1000).reduce(0) { $0+$1 }
newReduceSum

其他计算的一点的应用

函数混合示例: 使用中文变量😄

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
let 函数点阵密度 = 64

let 频率1 = 4.0
let 相位1 = 0.0
let 幅度1 = 1.0
let 正弦函数1 = (0..<函数点阵密度).map {
    幅度1 * sin(2.0 * M_PI / Double(函数点阵密度) * Double($0) * 频率1 + 相位1)
}

let 频率2 = 1.0
let 相位2 = M_PI / 2.0
let 幅度2 = 2.0
let 正弦函数2 = (0..<函数点阵密度).map {
    幅度2 * sin(2.0 * M_PI / Double(函数点阵密度) * Double($0) * 频率2 + 相位2)
}

let 频率3 = 10.0
let 相位3 = M_PI / 3.0
let 幅度3 = 4.0
let 正弦函数3 = (0..<函数点阵密度).map {
    幅度3 * sin(2.0 * M_PI / Double(函数点阵密度) * Double($0) * 频率3 + 相位3)
}

let 新函数1 = add(正弦函数1, y: 正弦函数2)
let 新函数2 = add(新函数1, y: 正弦函数3)

// Xcode 分栏查看图形排布，尤其是新函数的图形
新函数1.forEach { XCPlaygroundPage.currentPage.captureValue($0, withIdentifier:"新函数1") }
新函数2.forEach { XCPlaygroundPage.currentPage.captureValue($0, withIdentifier:"新函数2") }

正弦函数2.forEach { XCPlaygroundPage.currentPage.captureValue($0, withIdentifier:"正弦函数2") }

正弦函数1.forEach { XCPlaygroundPage.currentPage.captureValue($0, withIdentifier:"正弦函数1") }

傅里叶变换通俗篇讲解

1
2
3
// 查看图像发现‘新函数2’左右有三对波峰，得出它由三个正弦波组成（可对应得出振幅、频率及相位）
let 快速傅里叶转换 = fft(新函数2)
快速傅里叶转换.forEach { XCPlaygroundPage.currentPage.captureValue($0, withIdentifier:"快速傅里叶转换") }

矩阵计算

很多图像处理是根据矩阵做处理的，像素越大，处理性能要求越高

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 简单矩阵示例

// ⎛ 1  2 ⎞      ⎛ 3  2 ⎞       ⎛ 5  6 ⎞
// ⎢      ⎟  *   ⎢      ⎟   =   ⎢      ⎟
// ⎝ 3 -4 ⎠      ⎝ 1  2 ⎠       ⎝ 5 -2 ⎠

let A = Matrix([[1, 2], [3, -4]])
let B = Matrix([[3, 2], [1, 2]])
let C = A * B


// 利用逆矩阵求解
// ⎛ 1  1 ⎞        ⎛ 3 ⎞           ⎛ 2 ⎞
// ⎢      ⎟ * CC = ⎢   ⎟    CC =   ⎢   ⎟
// ⎝ 1 -1 ⎠        ⎝ 1 ⎠           ⎝ 1 ⎠

let AA = Matrix([[1, 1], [1, -1]])
let BB = Matrix([[3], [1]])
let CC = inv(AA) * BB

应用的加速库函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import Accelerate

public func sum(x: [Double]) -> Double {
    var result: Double = 0.0
    vDSP_sveD(x, 1, &result, vDSP_Length(x.count))

    return result
}

public func max(x: [Double]) -> Double {
    var result: Double = 0.0
    vDSP_maxvD(x, 1, &result, vDSP_Length(x.count))

    return result
}

public func mean(x: [Double]) -> Double {
    var result: Double = 0.0
    vDSP_meanvD(x, 1, &result, vDSP_Length(x.count))

    return result
}

public func add(x: [Double], y: [Double]) -> [Double] {
    var results = [Double](y)
    cblas_daxpy(Int32(x.count), 1.0, x, 1, &results, 1)

    return results
}

public func fft(input: [Double]) -> [Double] {
    var real = [Double](input)
    var imaginary = [Double](count: input.count, repeatedValue: 0.0)
    var splitComplex = DSPDoubleSplitComplex(realp: &real, imagp: &imaginary)

    let length = vDSP_Length(floor(log2(Float(input.count))))
    let radix = FFTRadix(kFFTRadix2)
    let weights = vDSP_create_fftsetupD(length, radix)
    vDSP_fft_zipD(weights, &splitComplex, 1, length, FFTDirection(FFT_FORWARD))

    var magnitudes = [Double](count: input.count, repeatedValue: 0.0)
    vDSP_zvmagsD(&splitComplex, 1, &magnitudes, 1, vDSP_Length(input.count))

    var normalizedMagnitudes = [Double](count: input.count, repeatedValue: 0.0)
    vDSP_vsmulD(sqrt(magnitudes), 1, [2.0 / Double(input.count)], &normalizedMagnitudes, 1, vDSP_Length(input.count))

    vDSP_destroy_fftsetupD(weights)

    return normalizedMagnitudes
}